ภาคเรียนที่ 1
ภาคเรียนที่ 2
เศษส่วนทศนิยมคู่อันดับและกราฟสมการการประมาณค่ารูปเรขาคณิตสองมิติและรูปเรขาคณิตสามมิติความน่าจะเป็นทักษะกระบวนการทางคณิตศาสตร์
บทที่ 1 สมบัติของจำนวนนับ
หน่วยการเรียนรู้ที่ 1 สมบัติของจำนวนนับ
1.เรื่อง การหาตัวประกอบ
จำนวนนับใดๆ ที่หารจำนวนนับที่กำหนดให้ได้ลงตัว เรียกว่า ตัวประกอบของจำนวนนับนั้น
ดังนั้น ครูสรุปให้นักเรียนฟังอีกครั้งว่า จำนวนนับที่เป็นตัวประกอบของ 18 คือ 1, 2, 3, 6, 9 และ 18
2.เรื่อง จำนวนเฉพาะ
วิธีการตรวจสอบว่า จำนวนใดเป็นจำนวนเฉพาะ โดยเทียบจากการนำจำนวนเฉพาะมายกกำลังสอง ผลลัพธ์ต้องน้อยกว่าจำนวนที่กำหนดให้ ครูยกตัวอย่างให้นักเรียนดู ดังนี้
ตัวอย่างที่ 1 ตรวจสอบว่า จำนวน 211 เป็นจำนวนเฉพาะหรือไม่
ขั้นที่ 1 พิจารณา 22 = 4
32 = 9
52 = 25
72 = 49
112 = 121
132 = 169
172 = 289
ขั้นที่ 2 พิจารณาจำนวนเฉพาะ 2, 3, 5, 7, 11, 13 ว่านำมาหาร 211 ลงตัว หรือไม่ (ไม่นำ 17 มาพิจารณา เพราะ 172 = 289 มากกว่า 211)
จะได้ว่า ไม่มีจำนวนเฉพาะใดหาร 211 ได้ลงตัว
ดังนั้น 211 เป็นจำนวนเฉพาะ
3.เรื่อง การแยกตัวประกอบ
ตัวอย่าง แยกตัวประกอบของ 150
ใช้การหาร
2 ) 150
3 ) 75
5 ) 25
5
ดังนั้น 150 = 2 x 3 x 5 x 5
วิธีนี้นำจำนวนเฉพาะที่น้อยที่สุดที่หารลงตัวมาเป็นตัวหารก่อน แล้วจึงนำ
จำนวนเฉพาะจำนวนถัดไปที่หารลงตัวมาหาร จนได้คำตอบสุดท้ายเป็น
จำนวนเฉพาะ
จำนวนเฉพาะจำนวนถัดไปที่หารลงตัวมาหาร จนได้คำตอบสุดท้ายเป็น
จำนวนเฉพาะ
4.เรื่อง การหา ห.ร.ม.
ตัวหารร่วมที่มากทีสุด (ห.ร.ม.)
ตัวหารร่วมที่มากที่สุดของจำนวนใดๆ ตั้งแต่ 2 จำนวนขึ้นไป หมายถึง จำนวนที่มีค่ามากที่สุดที่สามารถหารจำนวนทั้งหมดเหล่านั้นได้ลงตัว
ตัวหารร่วมที่มากที่สุดของจำนวนใดๆ ตั้งแต่ 2 จำนวนขึ้นไป หมายถึง จำนวนที่มีค่ามากที่สุดที่สามารถหารจำนวนทั้งหมดเหล่านั้นได้ลงตัว
วิธีการหา ห.ร.ม.
1. โดยการแยกตัวประกอบ มีิวิธีการดังนี้
(1) แยกตัวประกอบของจำนวนทุกจำนวนที่ต้องการหาร ห.ร.ม.
(2) เลือกตัวประกอบที่ซ้ำกันของทุกจำนวนมาคูณกัน
(3) ห.ร.ม. คือ ผลคูณที่ได้
1. โดยการแยกตัวประกอบ มีิวิธีการดังนี้
(1) แยกตัวประกอบของจำนวนทุกจำนวนที่ต้องการหาร ห.ร.ม.
(2) เลือกตัวประกอบที่ซ้ำกันของทุกจำนวนมาคูณกัน
(3) ห.ร.ม. คือ ผลคูณที่ได้
ตัวอย่าง จงหา ห.ร.ม. ของ 56 84 และ 140
วิธีทำ 56 =
84 =
104 =
เลือกตัวที่ซ้ำกัน ที่อยู่ทั้ง 56 84และ 104 ตัวทีซ้ำกันเอามาซ้ำละ 1 ตัว
คือ มีเลข 2 เลข 2 และ เลข 7
วิธีทำ 56 =
84 =
104 =
เลือกตัวที่ซ้ำกัน ที่อยู่ทั้ง 56 84และ 104 ตัวทีซ้ำกันเอามาซ้ำละ 1 ตัว
คือ มีเลข 2 เลข 2 และ เลข 7
ดังนั้น ห.ร.ม. =
2. การหารสั้น มีวิธีการดังนี้
1) นำจำนวนทั้งหมดที่ต้องการหา ห.ร.ม. มาเขียนเรียงกัน
2) หาจำนวนเฉพาะที่สามารถหารจำนวนทั้งหมดได้ลงตัวมาหารไปเรื่อยๆ จนกว่าไม่สามารถหาได้
3) นำตัวหารทุกตัวที่ใช้มาคูณกัน เป็นค่าของ ห.ร.ม.
1) นำจำนวนทั้งหมดที่ต้องการหา ห.ร.ม. มาเขียนเรียงกัน
2) หาจำนวนเฉพาะที่สามารถหารจำนวนทั้งหมดได้ลงตัวมาหารไปเรื่อยๆ จนกว่าไม่สามารถหาได้
3) นำตัวหารทุกตัวที่ใช้มาคูณกัน เป็นค่าของ ห.ร.ม.
ตัวอย่าง จงหา ห.ร.ม. ของ 56 84 และ 140
วิธีทำ 2) 56 84 104
2) 28 42 70
7) 14 21 35
2 3 5
วิธีทำ 2) 56 84 104
2) 28 42 70
7) 14 21 35
2 3 5
ห.ร.ม. คือ 2 x 2 x 7 = 28
ประโยชน์ของ ห.ร.ม.
1. ใช้ทอนเศษส่วนให้เป็นเศษส่วนอย่างต่ำ
2. ใช้คำนวณการแบ่งสิ่งของที่มีจำนวนไม่เท่ากันออกเป็นส่วนๆ ที่เท่าักันโดยไม่ปะปนกันและให้เป็นจำนวนที่มากที่สุด
1. ใช้ทอนเศษส่วนให้เป็นเศษส่วนอย่างต่ำ
2. ใช้คำนวณการแบ่งสิ่งของที่มีจำนวนไม่เท่ากันออกเป็นส่วนๆ ที่เท่าักันโดยไม่ปะปนกันและให้เป็นจำนวนที่มากที่สุด
5.เรื่อง การหา ค.ร.น.
ตัวคูณร่วมน้อยที่สุด (ค.ร.น.)
ตัวคูณร่วมน้อยที่สุดของจำนวนใดๆ ตั้งแต่ 2 จำนวนขึ้นไป หมายถึง จำนวนที่น้อยที่สุดที่จำนวนเหล่านั้นมาหารได้ลงตัว หรือจำนวนที่น้อยที่สุดที่มีจำนวนเหล่านั้นเป็นตัวประกอบ
ตัวคูณร่วมน้อยที่สุดของจำนวนใดๆ ตั้งแต่ 2 จำนวนขึ้นไป หมายถึง จำนวนที่น้อยที่สุดที่จำนวนเหล่านั้นมาหารได้ลงตัว หรือจำนวนที่น้อยที่สุดที่มีจำนวนเหล่านั้นเป็นตัวประกอบ
วิธีการหา ค.ร.น.
1. โดยการแยกตัวประกอบ มีวิธีการดังนี้
1) แยกตัวประกอบของจำนวนทุกจำนวนที่ต้องการหา ค.ร.น.
2) เลือกตัวประกอบตัวที่ซ้ำกันมาเพียงตัวเดียว
3) เลือกตัวประกอบตัวที่ไม่ซ้ำกันมาทุกตัว
4) นำจำนวนทีี่่่เลือกมาจากข้อ 2และ 3มาคูณกันทั้งหมด เป็นค่าของ ค.ร.น.
1. โดยการแยกตัวประกอบ มีวิธีการดังนี้
1) แยกตัวประกอบของจำนวนทุกจำนวนที่ต้องการหา ค.ร.น.
2) เลือกตัวประกอบตัวที่ซ้ำกันมาเพียงตัวเดียว
3) เลือกตัวประกอบตัวที่ไม่ซ้ำกันมาทุกตัว
4) นำจำนวนทีี่่่เลือกมาจากข้อ 2และ 3มาคูณกันทั้งหมด เป็นค่าของ ค.ร.น.
ตัวอย่าง จงหา ค.ร.น. ของ 10, 24 และ 30
วิธีทำ 10 =
24 =
30 =
วิธีทำ 10 =
24 =
30 =
ค.ร.น. = 5 x 2 x 3 x 2 x 2 = 120
2. โดยการหารสั้น มีวิธีการดังนี้
1) นำจำนวนทั้งหมดที่ต้องการหา ค.ร.น. มาตั้งเรียงกัน
2) หาจำนวนเฉพาะที่สามารถหารจำนวนทั้งหมดได้ลงตัว หรือหารลงตัวอย่างน้อย 2 จำนวน จำนวนใดหารไม่ได้ให้ดึงลงมา
3) ให้ทำซ้ำข้อ 2 จนกว่าจะหารอีกไม่ได้
4) นำตัวหารทั้งหมดและผลลัพธ์สุดท้ายมาคูณกัน ผลคูณคือค่าของ ค.ร.น.
1) นำจำนวนทั้งหมดที่ต้องการหา ค.ร.น. มาตั้งเรียงกัน
2) หาจำนวนเฉพาะที่สามารถหารจำนวนทั้งหมดได้ลงตัว หรือหารลงตัวอย่างน้อย 2 จำนวน จำนวนใดหารไม่ได้ให้ดึงลงมา
3) ให้ทำซ้ำข้อ 2 จนกว่าจะหารอีกไม่ได้
4) นำตัวหารทั้งหมดและผลลัพธ์สุดท้ายมาคูณกัน ผลคูณคือค่าของ ค.ร.น.
ตัวอย่าง จงหา ค.ร.น. ของ 10, 24 และ 30
วิธีทำ 2) 10 24 30
5) 5 12 15
3) 1 12 3
1 4 1
5) 5 12 15
3) 1 12 3
1 4 1
ค.ร.น. = 2 x 5 x 3 x 4 = 120
ประโยชน์ของ ค.ร.น.
1. ใช้ในการหาผลบวกและผลลบของเศษส่วน โดยทำส่วนให้เท่ากัน
2. ใช้ในการคำนวณงานบางอย่างที่ใช้เวลาต่างกัน และหาเวลาที่จะทำพร้อมกันในครั้งต่อไป
1. ใช้ในการหาผลบวกและผลลบของเศษส่วน โดยทำส่วนให้เท่ากัน
2. ใช้ในการคำนวณงานบางอย่างที่ใช้เวลาต่างกัน และหาเวลาที่จะทำพร้อมกันในครั้งต่อไป
ความสัมพันธ์ระหว่าง ห.ร.ม. และ ค.ร.น.
- ถ้า a, b เป็นจำนวนเต็มบวก และ c เป็น ห.ร.ม. ของ a, b
- จะได้ว่า ค.ร.น. ของ a และ b เท่ากับ ab หรือท่องว่า ห.ร.ม. x ค.ร.น. = เลข 2 จำนวนนั้นคูณกัน
ตัวอย่างจำนวนนับสองจำนวนมีผลคูณเท่ากับ 80 และมี ห.ร.ม.เท่ากับ 2 จงหา ค.ร.น.ของจำนวนทั้งสอง วิธีทำ ห.ร.ม. x ค.ร.น. =เลข 2 จำนวนคูณกัน 2 x ค.ร.น. = 80 - ค.ร.น = 40
เขียนใน เลขยกกำลัง
ธนาคารความรู้ การคูณเลขยกกำลัง
เลขยกกำลัง
คือ การคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) จะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa)
ตัวอย่าง
25 เป็นเลขยกกำลัง ที่มี 2 เป็นฐานหรือตัวเลข และมี 5 เป็นเลขชี้กำลัง
และ 25 = 2x2x2x2x2 = 32สมบัติของเลขยกกำลัง
1. สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เมื่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวกเช่น 23x 27x 29 = 2 (3 + 7 + 9) = 2192. สมบัติการหารเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวกกรณีที่ 1 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m > nเช่น 412÷ 43=412-3 = 49กรณีที่ 2 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, nเป็นจำนวนเต็มบวกที่ m = nนิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ a0 = 1เช่น 67÷ 67 = 67-7 = 60 = 1 หรือถ้า (-7)o = 1กรณีที่ 3เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m < n นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว3.สมบัติอื่นๆของเลขยกกำลัง1. เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง2. เลขยกกำลังที่มีฐานอยู่ในรูปการคูณ หรือการหารของจำนวนหลาย ๆจำนวน3. เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วน
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว3.สมบัติอื่นๆของเลขยกกำลัง1. เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง2. เลขยกกำลังที่มีฐานอยู่ในรูปการคูณ หรือการหารของจำนวนหลาย ๆจำนวน3. เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วนการใช้เลขยกกำลังแทนจำนวน
การเขียนจำนวนที่มีค่ามากๆนิยมเขียนแทนได้ด้วยรูป Ax10nเมื่อ 1≤A<10 และ n เป็นจำนวนเต็มบวก เช่น 16,000,000 = 1.6×107 และทำนองเดียวกันการเขียนจำนวนเต็มที่มีค่าน้อยๆก็สามารถเขียนในรูป Ax10n ได้เช่นเดียวกัน แต่ n จะเป็นจำนวนเต็มลบ เช่น 0.000016 = 1.6×10-5หลักการเปลี่ยนจำนวนให้อยู่ในรูป Ax10n เมื่อ 1≤A<10 และ n เป็นจำนวนเต็มอย่างง่ายๆ คือให้พิจารณาว่าจุดทศนิยมมีการเลื่อนตำแหน่งไปทางซ้ายหรือขวากี่ตำแหน่ง ถ้าเลื่อนไปทางซ้ายเลขชี้กำลังจะเป็นบวก และถ้าเลื่อนไปทางขวาเลขชี้กำลังก็จะเป็นลบเช่น 75000.0=7.5×1040.000075 = 7.5×10-5หรือกล่าวได้ว่า ถ้าจุดทศนิยมเลื่อนไปทางขวา n ตำแหน่ง เลขชี้กำลังของ 10 จะลดลง n ถ้าจุดทศนิยมเลื่อนไปทางซ้าย n ตำแหน่ง เลขชี้กำลังของ10 จะเพิ่มขึ้น nสรุป
เลขยกกำลังเป็นการคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) หรือจะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa) อีกทั้งวิธีการคำนวณหาค่าเลขยกกำลังจะขึ้นอยู่กับสมบัติของเลขยกกำลังในแต่ละประเภทด้วยการบวกเลขยกกำลัง
1.การบวกลบเลขยกกำลังที่มีฐานเหมือนกันและเลขยกกำลังเท่ากัน ให้นำสัมประสิทธิ์ของเลขยกกำลังมาบวกลบกัน2.การบวกลบเลขยกกำลังที่มีฐานเท่ากัน แต่เลขยกกำลังไม่เท่ากันจะนำสัมประสิทธิ์มาบวกลบกันไม่ได้ ต้องทำในรูปของการแยกตัวประกอบ และดึงตัวประกอบร่วมออกตัวอย่างหมายเหตุ(-2)4 และ -24 มีค่าไม่เท่ากันเพราะ (-2)4 ฐานคือ (-2)เลขชี้กำลังคือ 4 อ่านว่าลบสองทั้งหมดยกกำลังสี่มีค่าเท่ากับ 16-24 ฐานคือ 2 เลขชี้กำลังคือ 4 อ่านว่าลบของสองกำลังสี่มีค่าเท่ากับ -16



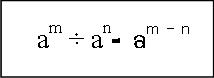





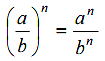
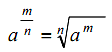


ไม่มีความคิดเห็น:
แสดงความคิดเห็น