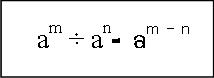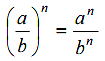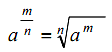หน่วยการเรียนรู้ที่ 1 สมบัติของจำนวนนับ
1.เรื่อง การหาตัวประกอบ
จำนวนนับใดๆ ที่หารจำนวนนับที่กำหนดให้ได้ลงตัว เรียกว่า ตัวประกอบของจำนวนนับนั้น
ดังนั้น ครูสรุปให้นักเรียนฟังอีกครั้งว่า จำนวนนับที่เป็นตัวประกอบของ 18 คือ 1, 2, 3, 6, 9 และ 18
2.เรื่อง จำนวนเฉพาะ
วิธีการตรวจสอบว่า จำนวนใดเป็นจำนวนเฉพาะ โดยเทียบจากการนำจำนวนเฉพาะมายกกำลังสอง ผลลัพธ์ต้องน้อยกว่าจำนวนที่กำหนดให้ ครูยกตัวอย่างให้นักเรียนดู ดังนี้
ตัวอย่างที่ 1 ตรวจสอบว่า จำนวน 211 เป็นจำนวนเฉพาะหรือไม่
ขั้นที่ 1 พิจารณา 22 = 4
32 = 9
52 = 25
72 = 49
112 = 121
132 = 169
172 = 289
ขั้นที่ 2 พิจารณาจำนวนเฉพาะ 2, 3, 5, 7, 11, 13 ว่านำมาหาร 211 ลงตัว หรือไม่ (ไม่นำ 17 มาพิจารณา เพราะ 172 = 289 มากกว่า 211)
จะได้ว่า ไม่มีจำนวนเฉพาะใดหาร 211 ได้ลงตัว
ดังนั้น 211 เป็นจำนวนเฉพาะ
3.เรื่อง การแยกตัวประกอบ
ตัวอย่าง แยกตัวประกอบของ 150
ใช้การหาร
2 ) 150
3 ) 75
5 ) 25
5
ดังนั้น 150 = 2 x 3 x 5 x 5
วิธีนี้นำจำนวนเฉพาะที่น้อยที่สุดที่หารลงตัวมาเป็นตัวหารก่อน แล้วจึงนำ
จำนวนเฉพาะจำนวนถัดไปที่หารลงตัวมาหาร จนได้คำตอบสุดท้ายเป็น
จำนวนเฉพาะ
4.เรื่อง การหา ห.ร.ม.
ตัวหารร่วมที่มากทีสุด (ห.ร.ม.)
ตัวหารร่วมที่มากที่สุดของจำนวนใดๆ ตั้งแต่ 2 จำนวนขึ้นไป หมายถึง จำนวนที่มีค่ามากที่สุดที่สามารถหารจำนวนทั้งหมดเหล่านั้นได้ลงตัว
วิธีการหา ห.ร.ม.
1. โดยการแยกตัวประกอบ มีิวิธีการดังนี้
(1) แยกตัวประกอบของจำนวนทุกจำนวนที่ต้องการหาร ห.ร.ม.
(2) เลือกตัวประกอบที่ซ้ำกันของทุกจำนวนมาคูณกัน
(3) ห.ร.ม. คือ ผลคูณที่ได้
ตัวอย่าง จงหา ห.ร.ม. ของ 56 84 และ 140
วิธีทำ 56 =
84 =
104 =
เลือกตัวที่ซ้ำกัน ที่อยู่ทั้ง 56 84และ 104 ตัวทีซ้ำกันเอามาซ้ำละ 1 ตัว
คือ มีเลข 2 เลข 2 และ เลข 7
ดังนั้น ห.ร.ม. =
2. การหารสั้น มีวิธีการดังนี้
1) นำจำนวนทั้งหมดที่ต้องการหา ห.ร.ม. มาเขียนเรียงกัน
2) หาจำนวนเฉพาะที่สามารถหารจำนวนทั้งหมดได้ลงตัวมาหารไปเรื่อยๆ จนกว่าไม่สามารถหาได้
3) นำตัวหารทุกตัวที่ใช้มาคูณกัน เป็นค่าของ ห.ร.ม.
ตัวอย่าง จงหา ห.ร.ม. ของ 56 84 และ 140
วิธีทำ 2) 56 84 104
2) 28 42 70
7) 14 21 35
2 3 5
ห.ร.ม. คือ 2 x 2 x 7 = 28
ประโยชน์ของ ห.ร.ม.
1. ใช้ทอนเศษส่วนให้เป็นเศษส่วนอย่างต่ำ
2. ใช้คำนวณการแบ่งสิ่งของที่มีจำนวนไม่เท่ากันออกเป็นส่วนๆ ที่เท่าักันโดยไม่ปะปนกันและให้เป็นจำนวนที่มากที่สุด
5.เรื่อง การหา ค.ร.น.
ตัวคูณร่วมน้อยที่สุด (ค.ร.น.)
ตัวคูณร่วมน้อยที่สุดของจำนวนใดๆ ตั้งแต่ 2 จำนวนขึ้นไป หมายถึง จำนวนที่น้อยที่สุดที่จำนวนเหล่านั้นมาหารได้ลงตัว หรือจำนวนที่น้อยที่สุดที่มีจำนวนเหล่านั้นเป็นตัวประกอบ
วิธีการหา ค.ร.น.
1. โดยการแยกตัวประกอบ มีวิธีการดังนี้
1) แยกตัวประกอบของจำนวนทุกจำนวนที่ต้องการหา ค.ร.น.
2) เลือกตัวประกอบตัวที่ซ้ำกันมาเพียงตัวเดียว
3) เลือกตัวประกอบตัวที่ไม่ซ้ำกันมาทุกตัว
4) นำจำนวนทีี่่่เลือกมาจากข้อ 2และ 3มาคูณกันทั้งหมด เป็นค่าของ ค.ร.น.
ตัวอย่าง จงหา ค.ร.น. ของ 10, 24 และ 30
วิธีทำ 10 =
24 =
30 =
ค.ร.น. = 5 x 2 x 3 x 2 x 2 = 120
2. โดยการหารสั้น มีวิธีการดังนี้
1) นำจำนวนทั้งหมดที่ต้องการหา ค.ร.น. มาตั้งเรียงกัน
2) หาจำนวนเฉพาะที่สามารถหารจำนวนทั้งหมดได้ลงตัว หรือหารลงตัวอย่างน้อย 2 จำนวน จำนวนใดหารไม่ได้ให้ดึงลงมา
3) ให้ทำซ้ำข้อ 2 จนกว่าจะหารอีกไม่ได้
4) นำตัวหารทั้งหมดและผลลัพธ์สุดท้ายมาคูณกัน ผลคูณคือค่าของ ค.ร.น.
ตัวอย่าง จงหา ค.ร.น. ของ 10, 24 และ 30
วิธีทำ 2) 10 24 30
5) 5 12 15
3) 1 12 3
1 4 1
ค.ร.น. = 2 x 5 x 3 x 4 = 120
ประโยชน์ของ ค.ร.น.
1. ใช้ในการหาผลบวกและผลลบของเศษส่วน โดยทำส่วนให้เท่ากัน
2. ใช้ในการคำนวณงานบางอย่างที่ใช้เวลาต่างกัน และหาเวลาที่จะทำพร้อมกันในครั้งต่อไป
ความสัมพันธ์ระหว่าง ห.ร.ม. และ ค.ร.น.
- ถ้า a, b เป็นจำนวนเต็มบวก และ c เป็น ห.ร.ม. ของ a, b
- จะได้ว่า ค.ร.น. ของ a และ b เท่ากับ ab หรือท่องว่า ห.ร.ม. x ค.ร.น. = เลข 2 จำนวนนั้นคูณกัน
ตัวอย่างจำนวนนับสองจำนวนมีผลคูณเท่ากับ 80 และมี ห.ร.ม.เท่ากับ 2 จงหา ค.ร.น.ของจำนวนทั้งสอง วิธีทำ ห.ร.ม. x ค.ร.น. =เลข 2 จำนวนคูณกัน 2 x ค.ร.น. = 80
- ค.ร.น = 40
-
เลขยกกำลัง
คือ การคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) จะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa)
ตัวอย่าง
25 เป็นเลขยกกำลัง ที่มี 2 เป็นฐานหรือตัวเลข และมี 5 เป็นเลขชี้กำลัง
และ 25 = 2x2x2x2x2 = 32
สมบัติของเลขยกกำลัง
1. สมบัติการคูณเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก เมื่อ a เป็นจำนวนใด ๆ และ m, n เป็นจำนวนเต็มบวก
เช่น 23x 27x 29 = 2 (3 + 7 + 9) = 219
2. สมบัติการหารเลขยกกำลังที่มีเลขชี้กำลังเป็นจำนวนเต็มบวก
กรณีที่ 1 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m > n
เช่น 412÷ 43=412-3 = 49
กรณีที่ 2 เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, nเป็นจำนวนเต็มบวกที่ m = n
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ a0 = 1
เช่น 67÷ 67 = 67-7 = 60 = 1 หรือถ้า (-7)o = 1
กรณีที่ 3เมื่อ a เป็นจำนวนจริงใดๆที่ไม่ใช่ศูนย์ และ m, n เป็นจำนวนเต็มบวกที่ m < n
เช่น

= 1/ 5
4-9
นิยาม ถ้า a เป็นจำนวนจริงใดๆ ที่ไม่ใช่ศูนย์ และ n เป็นจำนวนเต็มบวก แล้ว

หรือ

เช่น

หรือ

3.สมบัติอื่นๆของเลขยกกำลัง
1. เลขยกกำลังที่มีฐานเป็นเลขยกกำลัง

เมื่อ a ≥0 และ m, n เป็นจำนวนเต็ม
เช่น

2. เลขยกกำลังที่มีฐานอยู่ในรูปการคูณ หรือการหารของจำนวนหลาย ๆจำนวน

และ
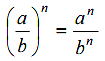
เมื่อ a ≠ 0 , b ≠ 0 และ n เป็นจำนวนเต็ม
เช่น

3. เลขยกกำลังที่มีเลขชี้กำลังเป็นเศษส่วน

เมื่อ a > 0 และ n เป็นจำนวนเต็มบวกที่มากกว่า 1
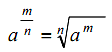
เมื่อ a ≠ 0 และ m เป็นจำนวนเต็มบวก ; n ≥ 2
การใช้เลขยกกำลังแทนจำนวน
การเขียนจำนวนที่มีค่ามากๆนิยมเขียนแทนได้ด้วยรูป Ax10nเมื่อ 1≤A<10 และ n เป็นจำนวนเต็มบวก เช่น 16,000,000 = 1.6×107 และทำนองเดียวกันการเขียนจำนวนเต็มที่มีค่าน้อยๆก็สามารถเขียนในรูป Ax10n ได้เช่นเดียวกัน แต่ n จะเป็นจำนวนเต็มลบ เช่น 0.000016 = 1.6×10-5
หลักการเปลี่ยนจำนวนให้อยู่ในรูป Ax10n เมื่อ 1≤A<10 และ n เป็นจำนวนเต็มอย่างง่ายๆ คือให้พิจารณาว่าจุดทศนิยมมีการเลื่อนตำแหน่งไปทางซ้ายหรือขวากี่ตำแหน่ง ถ้าเลื่อนไปทางซ้ายเลขชี้กำลังจะเป็นบวก และถ้าเลื่อนไปทางขวาเลขชี้กำลังก็จะเป็นลบ
เช่น 75000.0=7.5×104
0.000075 = 7.5×10-5
หรือกล่าวได้ว่า ถ้าจุดทศนิยมเลื่อนไปทางขวา n ตำแหน่ง เลขชี้กำลังของ 10 จะลดลง n ถ้าจุดทศนิยมเลื่อนไปทางซ้าย n ตำแหน่ง เลขชี้กำลังของ10 จะเพิ่มขึ้น n
สรุป
เลขยกกำลังเป็นการคูณตัวเลขนั้นๆตามจำนวนของเลขชี้กำลัง ซึ่งตัวเลขนั้นๆจะคูณตัวของมันเองและเมื่อแทน a เป็นจำนวนใด ๆ และแทน n เป็นจำนวนเต็มบวก โดยที่มี a เป็นฐานหรือตัวเลข และ n เป็นเลขชี้กำลัง(an) หรือจะได้ว่า a คูณกัน n ตัว (axaxaxaxax…xa) อีกทั้งวิธีการคำนวณหาค่าเลขยกกำลังจะขึ้นอยู่กับสมบัติของเลขยกกำลังในแต่ละประเภทด้วย
การบวกเลขยกกำลัง
1.การบวกลบเลขยกกำลังที่มีฐานเหมือนกันและเลขยกกำลังเท่ากัน ให้นำสัมประสิทธิ์ของเลขยกกำลังมาบวกลบกัน
ตัวอย่าง 
2.การบวกลบเลขยกกำลังที่มีฐานเท่ากัน แต่เลขยกกำลังไม่เท่ากันจะนำสัมประสิทธิ์มาบวกลบกันไม่ได้ ต้องทำในรูปของการแยกตัวประกอบ และดึงตัวประกอบร่วมออก
ตัวอย่าง
หมายเหตุ
(-2)4 และ -24 มีค่าไม่เท่ากันเพราะ (-2)4 ฐานคือ (-2)
เลขชี้กำลังคือ 4 อ่านว่าลบสองทั้งหมดยกกำลังสี่มีค่าเท่ากับ 16
-24 ฐานคือ 2 เลขชี้กำลังคือ 4 อ่านว่าลบของสองกำลังสี่มีค่าเท่ากับ -16